
When either the master item or the required parts are irregular-shaped (a situation often encountered in the leather, textile, metals industries) this is referred to as the nesting problem. Two-dimensional (2D) problems are encountered in furniture, clothing and glass production. One way is the dimensionality of the cutting: the above example illustrates a one-dimensional (1D) problem other industrial applications of 1D occur when cutting pipes, cables, and steel bars. It can also be computed that 19 different such solutions exist, each with 10 patterns and a waste of 0.401%, of which one such solution is shown below and in the picture:Ĭutting-stock problems can be classified in several ways. The optimal answer requires 73 master rolls and has 0.401% waste it can be shown computationally that in this case the minimum number of patterns with this level of waste is 10. There are 308 possible patterns for this small instance. Each master roll is 5600 mm, requiring a minimum of 72.7 rolls, which means 73 rolls or more are required.Ī minimum-waste solution, sequenced to minimise knife changes, shown as small white circles The total product required is 1380 x 22 + 1520 x 25 +. The problem therefore is to find an optimum set of patterns of making product rolls from the master roll, such that the demand is satisfied and waste is minimized.Ī simple lower bound is obtained by dividing the total amount of product by the size of each master roll.

The important thing about this kind of problem is that many different product units can be made from the same master roll, and the number of possible combinations is itself very large, in general, and not trivial to enumerate.
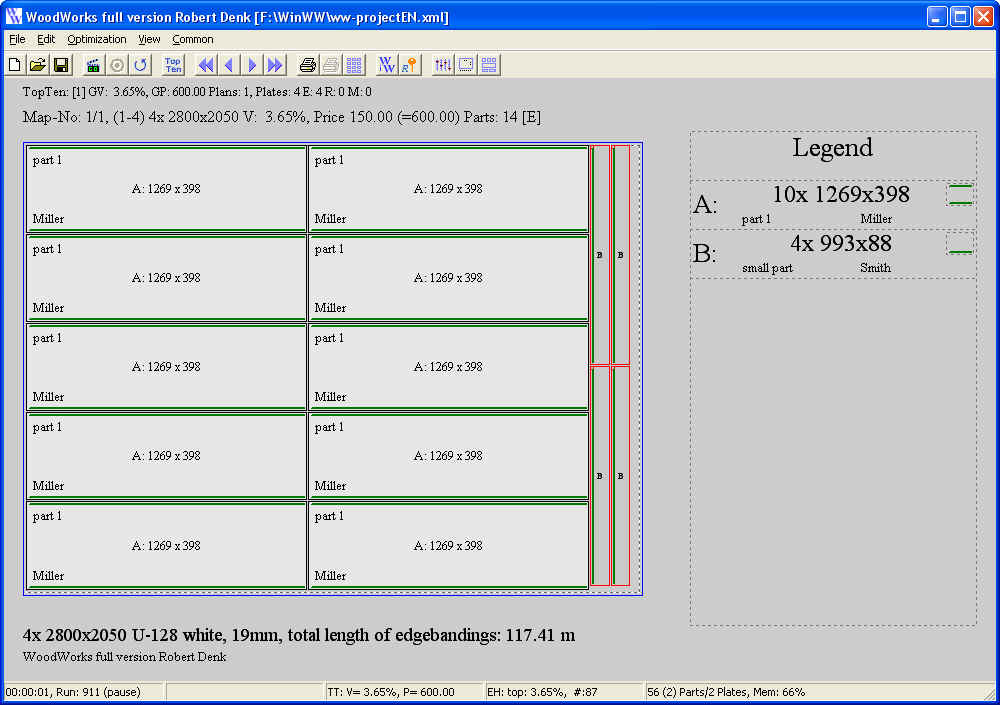
The following 13 items must be cut, in the table below. Illustration of one-dimensional cutting-stock problem Ī paper machine can produce an unlimited number of master (jumbo) rolls, each 5600 mm wide. 5 Mathematical formulation and solution approaches.1 Illustration of one-dimensional cutting-stock problem.


 0 kommentar(er)
0 kommentar(er)
